In this article, I’ll try and demystify text generation via neural networks by explaining how the technology works in very basic terms. Hopefully though, my explanation will be complete enough to give the reader an understanding that’s good enough to critically examine the hype around text generators and correct some misunderstandings I’ve seen around me. There’s also some terminology in there that will probably help you understand discussions on text generation (and also make you sound smarter☺).
So strap in, because we’ll be generating some text.
Generating Text: Evaluating
We’re going to attack this problem in reverse by first learning how text generation happens, and then examining how the system that generates our text was configured. It turns out the general process of text generation is much, much simpler than you think.
In this example, we’ll use a text generator that takes a single word as input (also called “prompt” in text generation), and outputs the next word based on its input. We’re using the neural network for completions.
In the most basic terms, every neural network is a gigantic equation. Evaluating that equation for your input gives you the next output. Let’s make it somewhat more concrete.
First, since equations work on numbers, we’ll need a way to pass words or text into those equations. This is something called an “embedding”. There are lots of different techniques for turning words into numbers, and I don’t know what technology ChatGPT et al. use for their embedding. For our purposes, we’ll use a very simple embedding:
| Word | Value |
|---|---|
| good | 1 |
| morning | 2 |
| afternoon | 3 |
| day | 4 |
| hello | 5 |
| how | 6 |
| are | 7 |
| you | 8 |
| doing | 9 |
You can see that we’ve just numbered some words in almost arbitrary order. Now, how do we generate
text? Let’s say we’re trying to complete “hello”. So we evaluate our equation with the value 5.
Let’s call the equation of our text generator f. We’ll learn more about the internals of the
equation in the next section, for now, let’s just evaluate it. Let’s say the output of the equation
for the input 5 (that is the word “hello”) is 6, which is the word “how”. Looks good, we might be generating the phrase “Hello, how are you doing”.
Simple enough, no? How do we generate sentences then? Well, first we need to extend our equation to take not only one input, but many, one for each word in the input sentence. This input is called “context”. Also, since our equation has a fixed number of inputs and sentences are not always of the same length, we need to define a “no word” value we can use to provide sentences shorter than the context size of the equation. Note that we still only have a single output, the next word.
Let’s say we want to have a context size of 4. Our equation now has 4 inputs: f(a, b, c, d). To get the next word for “hello”, we call f(5, 0, 0, 0) and receive the value 6 (“how”). We want to generate a complete sentence, so we feed back the value we just got into our equation. So far, we’ve gotten “hello how”, so we call f(5, 6, 0, 0) and get 7. We continue doing this until we evaluate f(5, 6, 7, 8) = 9, and we’ve gotten a complete sentence and decide to stop. We’ve generated the sentence “hello how are you doing” from the start word “hello”.
The salient point to take away from all this is that text generation isn’t magic: There’s no “learning” taking place here, the equation is not accessing the internet to search for facts, it isn’t alive. It’s just an equation that can output text that sounds plausible to human ears. Everything that’s magic is inside the equation, and it was put there during training. We’ll look at training later, but first let’s see how data can be transformed so that we can use it to configure a neural network.
Building a Corpus
This is where all the magic is put into our equation. In the rest of this section, I’m going to replace the term “training” with “adjusting” to make the whole terminology a bit more mundane. Adjusting an equation is significantly more involved than evaluating it, both conceptually and computationally, so hold on to your head coverings.
We’re reusing the embedding from above, including the “no word” value. Additionally, we need some data to adjust the equation to, the “corpus”. Our corpus is very simple, it’s just a few sentences.
Hello, how are you?
Good morning!
Good afternoon!
Good day!
Hello, how are you doing?
How are you doing?
In reality, corpora are much bigger, taken from Wikipedia, digitized books, forums and any other written source (often without the express consent of the rights holder, but what’re you gonna do?). We apply our embedding:
5 6 7 8
1 2
1 3
1 4
5 6 7 8 9
6 7 8 9
So far so good. Now, we need to convert this into input suitable for adjusting our equation. We’ve got a context size of 4, so we always need four inputs, and we want to generate the next word. When we don’t have a next word, we predict the “no word” value (which is the case for most of these sentences except one). So the data we use for adjusting our function looks as follows, with the input on the left and the expected output on the right.
5 6 7 8 | 0
1 2 0 0 | 0
1 3 0 0 | 0
1 4 0 0 | 0
5 6 7 8 | 9
6 7 8 9 | 0
What we want to do now is adjust our function to return the value on the right for every input. Doing this is the core loop of adjusting (or “training”, when talking about neural networks). But first, let’s delve deeper into the structure of our function.
Neural Network Details
The “function” we’ve been talking about so far is implemented as a neural network. A neural network consists of several neurons that are interconnected, often in a layered structure. Each neuron has weights, an activation function and a bias. Connections and activation functions are what makes up the architecture of a neural network. Most recent research has been focused on finding architectures that are useful for certain tasks. We’re going to be talking about a very simple network (barely even a network) though, so we won’t go into the specifics of neural network architectures. The weights and biases of each neuron make up the “knowledge” that is stored in a neural network.
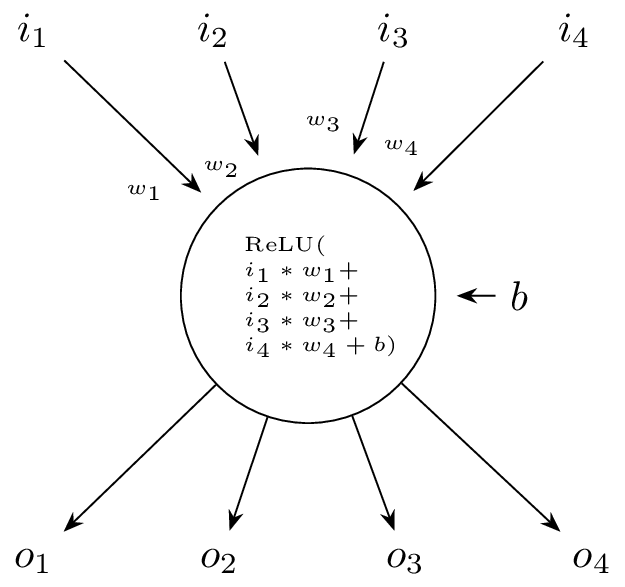
A diagram of our simple neuron
The figure above shows a single neuron with four inputs and four outputs. A “real” network would consist of a very large number of such neurons (in the billions of neurons), with outputs of each neuron connected to the inputs of other neurons (the neural network architecture).
If we use just a single neuron for our prediction, we can look at the function corresponding to the network. Remember we have four inputs and one output. This means our neuron has four weights and one bias. Connections are non-existent, and we use the ReLU activation function, which passes through the value if it’s greater than zero, and return zero otherwise.
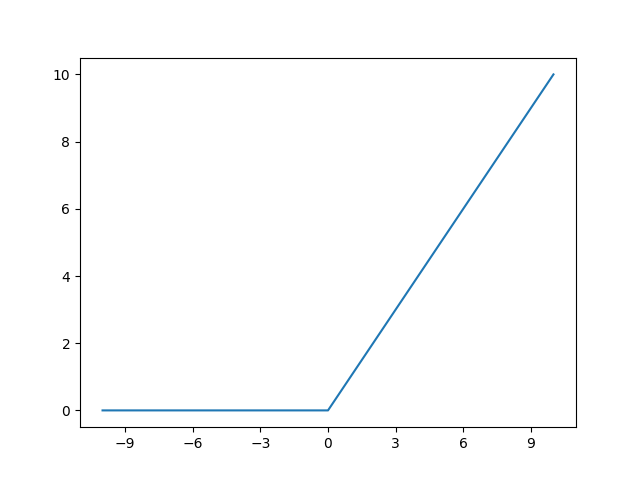
The ReLU function
Our neuron now corresponds to the following function, with w being the weights, and b the bias: f(a, b, c, d) = relu(w1 * a + w2 * b + w3 * c + w4 * d + b). Now we have an architecture, and can start adjusting our weights and biases with the corpus.
Note that in reality, neural networks have much more complex architectures. LLaMA, for example, has 65 billion parameters (weights and biases) in its largest configuration. All knowledge that the neural network has is encoded in these weights and biases, not in external databases or files.
Neural Network Training
For a first try, we can just choose the weights and bias randomly. Let’s try the following.
| Weight | Value |
|---|---|
| w1 | 0.5 |
| w2 | 0.3 |
| w3 | 0.8 |
| w4 | 0.1 |
| b | 2 |
Let’s now try the function for our corpus entry 5 6 7 8 | 0: f(5, 6, 7, 8) = relu(0.5 * 5 + 0.3 * 6 + 0.8 * 7 + 0.1 * 8 + 2) = 12.7. Now, that’s not exactly what we wanted (it’s not even a word in our corpus). How wrong is it, though? Neural network training uses something called a “loss function” to compute the quality of results. One of the simplest loss functions is the “mean squared error”, which is exactly what it sounds like: For our example, our predicted output was 12.7, while the correct output is 91. The error is 3.7, which is 13.69 squared. To calculate the mean squared error, we sum up the squared error for every element in our corpus and divide it by the number of elements in the corpus. Some quick calculation yields an error of 69.53̅, which is pretty bad.
However, now we can adjust our weights to reduce this error. We can do this with something called “gradient descent”. Gradient descent is a method for finding the minimum of a function by looking at the derivative (i.e. the “steepness”) of the function at a certain point, and then adjusting parameters to move in the direction of this gradient. As a real-life example, imagine how you can find the bottom of a mountain by going straight down the side of it. In our case, we want to find the minimum of the loss function, because that means our function has the smallest possible error on our corpus.
I’ll not try and do gradient descent here, as there’s several details that make it a bit more complicated. Suffice to say that training our network entails calculating the loss on our corpus (in our case, via the mean squared error), adjusting the weights via gradient descent, and then recalculating the loss function. For our simple single-neuron function, this is simple, but for larger networks, adjustments may need to be made to every neuron. Training a neural network is very computationally intensive, but it is the only way new knowledge can be encoded into its structure via updated weights.
For our examples, I’ve cheated a bit and used a mathematics application to find some weights based on the minimum square errors:
| Weight | Value |
|---|---|
| w1 | 0 |
| w2 | 0 |
| w3 | -81 |
| w4 | 72 |
| b | 0 |
Calculating the mean error for our corpus with these weights gives us 13.5, which is much better. Let’s see how it does!
f(5, 6, 7, 8) = 9
f(1, 2, 0, 0) = 0
f(1, 4, 0, 0) = 0
This looks pretty good. If not for the first entry in the corpus, this would be a perfect reproduction of what we want2, but we’ll take it. Now, the function reproduces our corpus pretty well. But does it generalize? What next word would it generate for “good morning how are”? The answer is 18, which is not a word. So our example is pretty much unuseable for any sentence that’s not in our corpus.
The boundaries of our example
As you can see, our example isn’t very useful as an actual text generator. We’ve used only a single neuron (which means that the network can only represent very simple functions), we’ve only used a single output, and our embedding is… basic, to say the least. Let’s look at these three parts, and how “real” neural networks implement them to generate “proper” text.
First, the architecture of the neural net. We only used a single neuron with four weights. “Real” networks use many more neurons — for ChatGPT 2, the number is about 50 billion. This corresponds to about 1.5 billion parameters (weights and biases), along with a hand-tuned selection of activation functions. Additionally, connections between neurons are carefully designed to help the network fulfill its function. With this large number of parameters, a neural network is able to represent functions that are much more complex than our simple example.
Another limitation of our model is the single output. I’ve chosen it to make explaining the technology more palatable, but in reality, text generators don’t have a single output, but many. For our simple example, there would be 10 outputs (one for every embedding value), and the outputs value would represent the probability of this word being the next word. A sample training input would then look like 5 6 7 8 | 0 0 0 0 0 0 0 0 0 1, because for the sentence “hello how are you”, the word “doing” should have the probability 13. You can also see how this solves our problem of the function generating values that are not in the corpus we encountered in the previous section: Now, it can only return words that are in the corpus via their probabilities.
And finally, the embedding we used. As mentioned previously, embeddings are normally much more powerful. If we used the encoding from the previous paragraph in reality, it would require one output for every word in the english language. By embedding words into a smaller space, we can reduce the sizes of inputs and outputs. Additionally, embeddings embed words that have similar meaning in similar values — you could imagine “morning”, “afternoon” and “day” in our embedding to have this property as well, because they refer to related concepts, and have embedding values that are close to each other (2, 3 and 4). When the neural network function receives some input that is close to other input, it might generate output that is close to other training output.
What we have done with our example, where we are only able to reproduce training input, but input outside of the training data generates rubbish, is “overfitting” our function. This is when the weights are adjusted to exactly reproduce the training input, and nothing more4. In general, steps need to be taken to prevent this occurence, and let the network “generalize”. From my limited understanding, the ability to generalize primarily from a networks architecture and the training approach. But at the same time, recall that we’re still “only” training a gigantic mathematical function. The networks ability to “generalize” (i.e. generate text for any input, not only that in the training data) stems from finding numerical relations between values that may not have any real-world correspondence, but can be extracted from the training data.
Let’s take a quick detour into philosophy: We’ve trained a very simple function to deliver us output based on a corpus. The process on how to generate this output could be called “knowledge”. But the entire “knowledge” that we’ve generated is encoded in the weights of the function. This is very different from what we humans generally think of as knowledge (at least on a conscious level, the brain is a complicated beast). There is no way for someone to look at a set of weights and say “ah, I know what this does”. It is an opaque heap of numbers that does certain things correctly under certain circumstances. Outside those circumstances, this “knowledge” might be completely useless.
On firmer ground, the very simple mechanics I’ve used above are actually at the core of all the “AI” applications. With different embeddings5 and modified architectures, the general concepts of neural networks remain the same, for image generation, speech-to-text, text-to-speech, what have you.
Fin
So, let’s recap the important points:
- A neural network is basically a very large equation that takes your input and generates output.
- All “knowledge” of the network was encoded in the weights at training time. The weights don’t change without training again, and training is a computationally expensive process. ChatGPT doesn’t learn while you’re talking to it6.
- The “knowledge” of a neural network can’t be extracted from it by examining the weights. There is currently no way to get from a set of weights to a human-readable description of what the network does.
- All this technology is not (very) new. What is new is advances in hardware that have made the training and operation of very large neural networks possible. “Quantity has a quality all of its own” has never been truer.
A short disclaimer: I’ve skipped lots of details (batching and cross-validation, different loss functions, data augmentation, architectures, encodings and many more). I hope this article has still been useful for understanding the very general function of neural networks, and helps discredit some very common misconceptions about their inner workings.
-
Or zero, but I’m skipping
somea lot of detail here, so bear with me. In this case, we want 9. ↩︎ -
Normally, text generation networks don’t output a single word, but a probability distribution over all possible words. In our case, the output for 5, 6, 7, 8 (“hello how are you”) would be 50% probability for 9 (“doing”) , and 50% probability for 0 (sentence end). ↩︎
-
This encoding is called “one-hot” encoding, because there is always one value that’s one, while all others are zero. ↩︎
-
Normally, you split your data into two parts, one to train the network and one to check the loss. This approach is called cross-validation, and reduces the danger of overfitting by a lot. ↩︎
-
Actually, image embeddings are much simpler, in that you just have to rescale the image to a fixed size and encode the color as a single number. Then you can use it directly as input. ↩︎
-
It always receives the whole conversation as context, which is why it can “remember” stuff you or it have previously said to it, but that’s very much different from what I would consider “learning”. ↩︎